Definition
In this chapter we explore the most basic type of a limit in Real Analysis, that is the limit of a sequence of real numbers.
Since we will consider only sequences of real numbers we will usually say "sequence" instead of "sequence of real numbers". Whenever we consider sequences whose values are not real numbers, we will mention this explicitly.
We will often use the following expression:
What we mean by this is that we consider the sequence $f: \N \to \R$ defined by $$ f(n)= x_n\quad\text{for}\quad n\in\N. $$
Let $$ x_1, x_2, \ldots, x_n,\ldots $$ be a sequence. The real numbers $x_1, x_2, \ldots, x_n,\ldots$ are called the terms of the sequence; $x_1$ is the first term of the sequence, $x_2$ is the second term of the sequence, $\ldots,$ $x_n$ is the $n$th term of the sequence.
- $1, 2, 3, 4,\ldots,n\ldots;$
- $1\dfrac{1}{2},\dfrac{1}{3}\ldots,\dfrac{1}{n}\ldots;$
- $1\dfrac{1}{2^2},\dfrac{1}{3^2}\ldots,\dfrac{1}{n^2}\ldots;$
- $a, a^2, a^3, a^4,\ldots,a^n\ldots$ (with $a\in \R$);
- $1, 1, 1, 1,\ldots,1\ldots;$
-
$c, c, c, c,\ldots,c\ldots$ (with $c\in \R$);
Note: The sequence in (f) is called the constant sequence $c;$ hence the sequence (e) is the constant sequence $1.$ - $1, 0, 1, 0, 1, 0,\ldots;$
- $1, 4, 9, \ldots,n^2\ldots;$
- $-1, 1, -1, 1,\ldots,(-1)^n\ldots;$
Instead of writing $$ x_1, x_2, \ldots, x_n,\ldots $$ we will sometimes write
For instance $\left\{1/n\right\}_{n\in N}$ is the sequence in Example 1-(b). The sequence $\{b_k\}_{k\in\N},$ where $b_k=1$ if $k$ is odd and $b_n=0$ if $k$ is even, is the sequence in Example 1-(g).
Practice! Re-write the rest of the sequences from Example 1.
Hint
a. $\{n\}_{n\in\N}\,$ or $\,\{n\}_{n=1}^{\infty}\,$ or $\,\{k\}_{k\in\N}.$
The notation for a sequence is similar to that of a set. However, the notions are different. For instance, the sequence $\{ {(-1)}^n \}$ is the sequence $$-1,1,-1,1,-1,1,\ldots$$ whereas the set of values, the range of the sequence, is just the set $\{ -1, 1 \}.$ We can write this set as $\{ {(-1)}^n : n \in \N \}.$ When ambiguity can arise, we use the words sequence or set to distinguish the two concepts.
Convergence of sequences
The following is one of the most fundamental concepts in this real analysis. You need to make sure you understand it thoroughly and you must be able to use it comfortably.
The illustration in Figure 1 can be a useful aid to understand the notion of limit in $\R.$ We obtain this illustration by "plotting" the terms of the given sequence on the real line. In doing so, one must be aware that the same real number may appear more than once in the sequence. When we say that the sequence $\{x_n\}$ converges to $L\in \R$ we mean that if for every $\epsilon$ we consider the interval $\left(L-\epsilon, L+\epsilon\right),$ then there exists $N\in\N$ such that all the terms $x_n$ belong to $\left(L-\epsilon, L+\epsilon\right)$ whenever $n\geq N.$
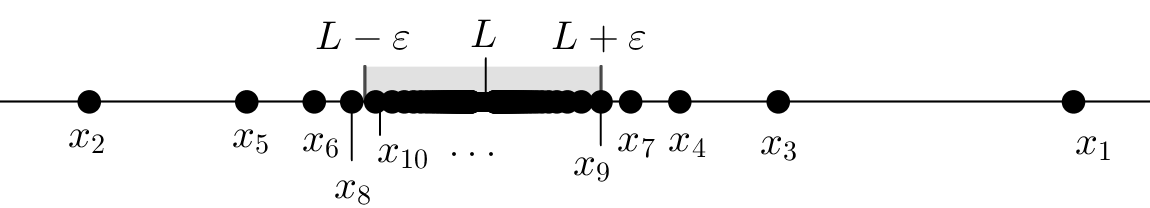
Another way to represent the converge of a sequence is shown in the applet below. In this image we first think of the sequence as a graph, as it is a function of $\N.$
Claim: The sequence $\left\{ \dfrac{1}{n} \right\}$ is convergent and \begin{equation*} \lim_{n\to \infty} \frac{1}{n} = 0 . \end{equation*}
Proof. Given an $\vre > 0,$ we find an $N \in \N$ such that $0 \lt \dfrac{1}{N} \lt \vre$ (thanks to the Archimedean property If \( x, y \in \mathbb{R} \) and \( x > 0 \), then there exists an \( n \in \mathbb{N} \) such that \( nx > y \). 😎).
You can recall the More information can be found in any Calculus book.
More information can be found in any Calculus book.
Then for all $n \geq N,$
Before proceeding further, we should give two examples of sequences which are divergent (not convergent) in $\R.$
Claim: The sequence $\{ n \}_{n\in\N}$ is not convergent.
Proof. Suppose that the sequence $1, 2, 3,\ldots $ converges to some number $y\in \R.$ Then given $\epsilon = \dfrac{1}{3},$ there exists a $M\in\N$ such that
In particular,
since $M+1\gt M.$ We deduce that
that is $$1\lt \frac{2}{3}.$$ Since the hypothesis that $1,2,3,\ldots$ converges in $\R$ leads to a contradiction we conclude that this sequence does not converge in $\R.$
Claim: The sequence $\{ {(-1)}^n \}$ is divergent.
Proof. If there were a limit $L,$ then for $\vre = \dfrac{1}{2}$ we expect an $N$ that satisfies the definition.
Suppose such an $N$ exists. Then for an even $n \geq N$ we compute $$\ds \frac{1}{2} > \abs{x_n - L} = \abs{1 - L}$$ and $$ \frac{1}{2} > \abs{x_{n+1} - L} = \abs{-1 - L} .$$ But $$\ds 2 = \abs{1 - L - (-1 -L)} \leq \abs{1 - L} + \abs{-1 -L}\lt\frac{1}{2}+\frac{1}{2}=1$$ which is a contradiction!
Therefore, the sequence $\{ {(-1)}^n \}$ is divergent.
The proof of the following theorem shows another useful technique in analysis. Many proofs in real analysis follow the same general scheme. In this case, we want to show a certain quantity is zero. Using the triangle inequality we write the quantity as two quantities, and then we estimate each one by arbitrarily small numbers.
Intuitive vs Rigorous proofs of limits
Let's see one more example of proof using the definition of the limit of a sequence. With a little study and practice, you should be able to do proofs of this sort yourself.
Show that
$$\lim_{n\ra \infty} \frac{n+1}{n} = 1.$$ Discussion: Our task here is to consider an arbitrary $\vre$ and show that there exists a number $N\in \N$ (which will depend on $\vre$) such that $n\geq N$ implies $$\abs{\frac{n+1}{n}-1} \lt \vre .$$ So we expect our formal proof to begin with "Let $\vre> 0 $ be arbitrary" and to end with something like "Hence $n \geq N$ implies $\abs{\frac{n+1}{n}-1} \lt \vre .$" In between the proof we should specify an $N\in \N$ with a particular property and then verify that for every $n \geq N$ implies \[ \abs{\frac{n+1}{n}-1} \lt \vre. \]
We will initially work backward from our desired conclusion, but in the formal proof we will have to be sure our steps are reversible. In the present example, we want $$\abs{\frac{n+1}{n}-1} \lt \vre$$ and we want to know how big $n$ must be. So we will operate on this inequality algebraically and try to "solve" for $n.$ In this case, since $$\abs{\frac{n+1}{n}-1}=\frac{1}{n}\lt\vre,$$ then we want $n> \dfrac{1}{\vre}.$ Thus, if our steps are reversible, choosing $N\in \N$ to be greater than $\dfrac{1}{\vre}$ implies \[ \abs{\frac{n+1}{n}-1} \lt \vre. \] With this observation, we are ready to write the formal argument.
The definition of convergence given above is the result of hundreds of years of refining the intuitive notion of limit into a mathematically rigorous statement. The logic involved is complicated and is intimately tied to the use of the quantifiers "for all" and "there exists". Learning to write a mathematically correct convergence proof goes hand in hand with a deep understanding of why the quantifiers appear in the order that they do.
The definition begins with the phrase
"For every $\vre>0,$ there exists $N\in \N$ such that ..."
Looking at Example 6, we see that our formal proof begins with, "Let $\vre>0$ be an arbitrary number." This is followed by a construction of $N$ and then a demonstration that this choice of $N$ has the desired property. This, in fact, is a basic outline for how every convergence proof should be presented:
Template for a proof that $\ds \lim_{n\to\infty} {x_n} = L$
- "Let $\vre >0 $ be arbitrary."
- Demonstrate a choice for $N \in \N.$ This step usually requires the most work, almost all of which is done prior to actually writing the formal proof.
- Now, show that $N$ actually works.
- "Assume $n\geq N.$"
- With $N$ well chosen, it should be possible to derive the inequality $\abs{x_n - L}\lt\vre.$
Bounded sequences
- A sequence $\{ x_n \}$ is bounded above if there exists a $ B\in \R$ such that $x_n\leq B$ for all $n\in \N.$
- A sequence $\{ x_n \}$ is bounded below if there exists a $ B\in \R$ such that $B \leq x_n $ for all $n\in \N.$
- A sequence $\{ x_n \}$ is bounded if there exists a $B \in \R$ such that \begin{equation*} \abs{x_n} \leq B \qquad \text{for all } n \in \N. \end{equation*}