Definition
When $f \colon S \to \R$ is continuous at all $c \in S,$ then we simply say $f$ is a continuous function.
Consider a function $f \colon S \to \R$ defined on a set $S \subseteq \R$ and let $c \in S.$ Then
- If $c$ is not a cluster point of $S,$ then $f$ is continuous at $c.$
- If $c$ is a cluster point of $S,$ then $f$ is continuous at $c$ if and only if the limit of $f(x)$ as $x \to c$ exists and \begin{equation*} \lim_{x\to c} f(x) = f(c) . \end{equation*}
- The function $f$ is continuous at $c$ if and only if for every sequence $\{ x_n \}$ where $x_n \in S$ and $\lim\, x_n = c,$ the sequence $\{ \,f(x_n) \}$ converges to $f(c).$
For any $\epsilon > 0,$ simply pick this given $\delta.$ The only $x \in S$ such that $\abs{x-c} \lt \delta$ is $x=c.$ \[\Ra \;\abs{\,f(x)-f(c)} = \abs{\,f(c)-f(c)} = 0 \lt \epsilon.\]
Now let's prove item 2. Suppose $c$ is a cluster point of $S.$ $\nec$ First suppose $f$ is continuous at $c.$ For every $\epsilon > 0,$ there exists a $\delta \gt 0$ such that for $x \in S$ where $\abs{x-c} \lt \delta\;$ $\Ra \;\abs{\,f(x)-f(c)} \lt \epsilon.$ This is true since $x \in S \setminus \{ c \} \subset S.$ Therefore, $\lim_{x\to c} f(x) = f(c).$
Now let's prove the other direction. Again we assume $c$ is a cluster point of $S.$ $\suf$ Now assume that the limit of $f(x)$ as $x \to c$ exists and $\lim_{x\to c} f(x) = f(c).$ Then for every $\epsilon > 0,$ there is a $\delta \gt 0$ such that if $x \in S \setminus \{ c \}$ and $\abs{x-c} \lt \delta\,$ $\,\Ra \abs{\,f(x)-f(c)} \lt \epsilon.$ In particular $\abs{\,f(c)-f(c)} = 0 \lt \epsilon,$ and the definition of continuity at $c$ is satisfied.
Discontinuity criterion
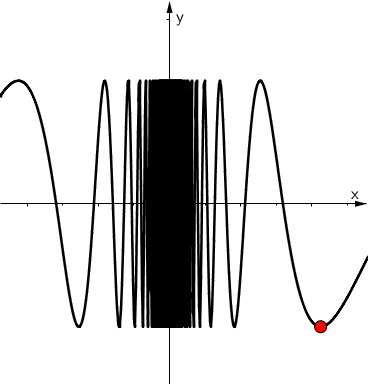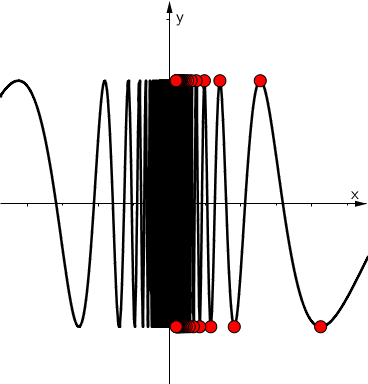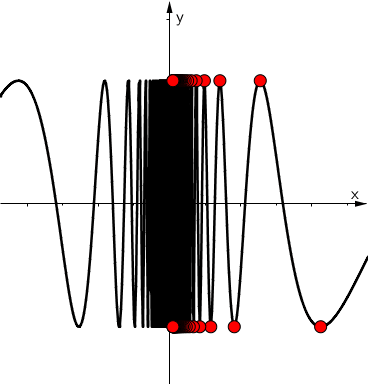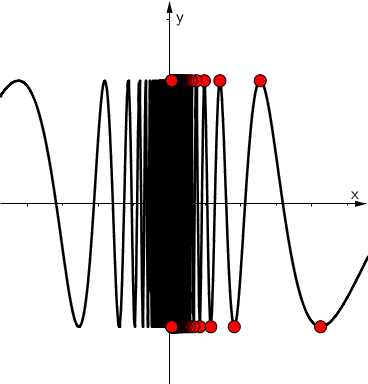
Basic properties
- The function $h \colon S \to \R$ defined by $h(x) := f(x)+g(x)$ is continuous at $c.$
- The function $h \colon S \to \R$ defined by $h(x) := f(x)-g(x)$ is continuous at $c.$
- The function $h \colon S \to \R$ defined by $h(x) := f(x)g(x)$ is continuous at $c.$
- If $g(x)\not=0$ for all $x \in S,$ the function $h \colon S \to \R$ defined by $h(x) := \dfrac{f(x)}{g(x)}$ is continuous at $c.$
Claim: The functions $\sin(x)$ and $\cos(x)$ are continuous.
Proof.
Recall that
$\abs{\sin(x)} \leq \abs{x},$ $\abs{\cos(x)} \leq 1,$
and $\abs{\sin(x)} \leq 1.$
Then
On the other hand we have
Using previous inequalities and applying the definition of continuity we can conclude that the functions $\sin(x)$ and $\cos(x)$ are continuous.
Uniform continuity
Proof. Note that $0 \leq x,c \leq 1.$ Then
Therefore, given $\epsilon > 0,$ let $\delta := \dfrac{\epsilon}{2}.$ If $\sabs{x-c} \lt \delta,$ then $\sabs{x^2-c^2} \lt \epsilon.$
On the other hand, $g \colon \R \to \R$ defined by $g(x):=x^2$ is not uniformly continuous.
Proof. Suppose it is uniformly continuous, then for every $\epsilon > 0,$ there would exist a $\delta > 0$ such that if $\sabs{x-c} \lt \delta,$ then $\sabs{x^2 -c^2} \lt \epsilon.$ So consider $\epsilon =1.$ If such $\delta$ existed and $c = x+ \delta/2$ $\;\Ra \ds\sabs{x^2 - \left(x+ \frac{\delta}{2}\right)^2} \lt 1.$ However $ \ds \abs{x\delta + \dfrac{\delta^2}{4}} \lt 1$❗ which is a contradiction, since we can choose $x$ large.
Proof. Choose $\epsilon=2$ and $0 \lt \delta.$ Set $\delta_0 = \min\{\delta/2, 1/4\}$, $x= \delta_0$, and $y = 2 \delta_0.$ Then $x,y\in(0,1)$ and $\abs{x-y}= \delta_0 \lt \delta$ but
Hence $f$ is not uniformly continuous.
More coming soon!